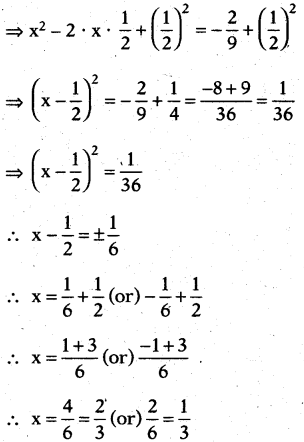Quadratic Equations

4th Lesson Quadratic Equations Class 10 Important Questions with Solutions

10th Class Maths Quadratic Equations 1 Mark Important Questions

Question 1.
Find the quadratic equation whose roots are 2 + √3 and 2 - √3 .

Solution:
α = 2 + √3
β = 2 - √3
The quadratic equation is
k(x² - (α + β)x + αβ) = 0
k(x² - (2 + √3 + 2 - √3)x + (2 + √3)(2 - √3)) = 0
x² - 4x + 4- 3 = 0 (∵ k = 1)
x² - 4x + 1 = 0

Question 2.
What are the roots the quadratic equation x² - 0.04 = 0 ?

Solution:
x² - 0.04 = 0 ⇒ x = 0.04
x = √0.04 ⇒ x = ± 0-2

Question 3.
If the quadratic equation x² - 2x + k = 0 has equal roots, then value of k is ...... .

Solution:
x² - 2x + k = 0 has equal roots
b² = 4ac
(-2)² = 4(1) k
4 = 4k
k = 1

Question 4.
The values(s) of k for which the roots of quadratic equation x² + 4x + k = 0 are real, is:

Solution:
x² + 4x + k = 0
roots are real
b² - 4ac > 0
(4)² - 4(1) (k) ≥ 0
16 ≥ 4k
⇒ 4 ≥ k
⇒ k ≤ 4

Question 5.
The two roots of the equation 3x² - 26x + 2 = 0 are :

A) real and distinct
B) not real
C) real and equal
D) rational

Solution:
C) real and equal
3x² -2√6x + 2 = 0
b² - 4ac = (-2√6 )² - 4(3) (2)
= 24 - 24
= 0
∴ roots are real and equal.

Question 6.
Find the value of k, for which one of the root of the quadratic equation kx² - 14x + 8 = 0 is six times the other.

Solution:
α + 6α = -(-14)/k
7α = 14/k ⇒ k = 14/7α = 2/α
α.6α = 8/k
6α² = 8/k
6(2/k)² = 8/k
6×4/k2 = 8/k
⇒ 6/k = 2
k = 3

Question 7.
Write a quadratic equation with roots 3 and 4.

Solution:
x² - 7x + 12 = 0

Question 8.
Which of the following is not a quadratic equation ?

A) 2 (x - 1)² = 4x² - 2x + 1
B) 2x - ² = x² + 5
C) (√2x + √3)² + x² = 3x² - 5x
D) (x² + 2x)² = x⁴ + 3 + 4x³

Solution:
C) (√2x + √3)² + x² = 3x² - 5x
(√2x)² + 2 . √2x . √3 + (√3)² + x² = 3x² - 5x.
2x² + 3 + 2√6x + x² = 3x² - 5x
5x + 2√6x + 3 = 0
It is not a quadratic equation.

Question 9.
Find the discriminant of the quadratic equation 2x² - 5x - 3 = 0.

Solution:
2x² - 5x - 3 = 0
b² - 4ac = (-5)² - 4(2) (-3)
= 25 + 24
= 49

Question 10.
If the quadratic equation 9x² + bx + 1/4 = 0 has equal roots, then the value of b is :

Solution:
9x² + bx + 1/4 = 0
b² - 4ac = 0
b² - 4(9) (1/4) = 0
b² - 9 = 0
b = ±3

Question 11.
Draw the rough graph of the quadratic equation ax² + bx + c = 0, when b² - 4ac < 0.

Solution:

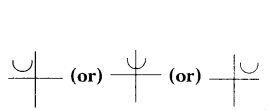
Question 12.
Write the sum of the roots of x² - 2024 = 0.

Solution:
α + β = -b/a = 0/1 = 0.

Question 13.
If x + 1/x = 2 then x² - 2x + 1 = ....... .

Solution:
x + 1/x = 2
x2+1/x = 2
x² - 2x + 1 = 0

Question 14.
The positive root value of 9 = √3x²+6 is ....... .

Solution:
9 = √3x²+6
81 = 3x² + 6
3x² = 75
⇒ x² = 25
⇒ x = ±5
but x = 5 only

Question 15.
If x = -1/2 is a solution of the quadratic equation 3x² + 2kx - 3 = 0 then k = ...... .

Solution:
3x² + 2kx - 3 = 0
x = -1/2
3(-1/2)2 + 2k(-1/2) - 3 = 0
3/4 - k - 3 = 0
⇒ -k = 3 - 3/4
-k = 12-3/4
⇒ -k = 9/4
k = -9/4

Question 16.
What is the quadratic equation whose roots are 1 - √2 and 1 + √2 ?

Solution:
α = 1 + √2, β = 1 - √2
x² -(α + β)x + αβ = 0
x² - 2x - 1 = 0 [∵ α + β = 1 + √2 + 1 - √2 = 2
αβ = 1² - (√2)² = 1 - 2 = -1]

Question 17.
Write the sum of the roots of 2024 - x² = 0.

Solution:
2024 - x² = 0
α + β = -b/0 = 0/-1 = 0

Question 18.
If one root of the quadratic equation 6x² - x + k = 0 is 2/3 then k = ...... .

Solution:
6x² - x + k = 0
6 (2/3)² - 2/3 + k = 0
6 × 4/9 - 2/3 = -k
2×4/3 - 2/3 = -k
8-2/3= -k
6/3 = -k
k = -2

Question 19.
Identify the quadratic equation from the following.

A) (4 - x)² = x² + 1
B) (2x + 1)² = (1 - 2x)²
C) (x + 1)²2 = -75
D) (9 - x)² = (9 + x)² - 3

Solution:
C) (x + 1)² = -75
Let (x + 1)² = -75
x² + 2x + 1 = -75
x² + 2x + 76 = 0

Question 20.
Which of the following quadratic equation has ‘1’ as a root ?

A) 9 - 3x² = 0
B) 4x² - 3 = 0
C) x² - 1 = 0
D) x² + 1 = 0

Solution:
C) x² - 1 = 0
1² - 1 = 0
0 = 0

Question 21.
Find the discriminant of x² - bx + k = 0.

Answer:
b² - 4k

Question 22.
If x = 0.2 is a root of the equation x² - 0.4k = 0 then k = ...... .

Solution:
x² - 0.4k = 0
(0.2)² - 0.4k = 0
(0.2)² = 0.4k
k = 0.04/0.4 = 0.1

Question 23.
Assertion (A) : The roots of x² - 1 = 0 are 1 and 2.
Reason (R) : The roots of ax² + bx + c = 0 are equal if b² - 4ac = 0

A) Assertion (A) is true, Reason (R) is true and R is the correct explanation of A.
B) Assertion (A) is true, Reason (R) is true but R is not the correct explanation of A.
C) A is true, R is false.
D) A is false, R is true.

Answer:
D) A is false, R is true.

Question 24.
Assertion (A) : (x + 2)² = x² + 1 is a quadratic equation.
Reason (R) : ax² + bx + c = 0 is the standard form of the quadratic equation.

A) Assertion (A) is true, Reason (R) is true and R is the correct explanation of A.
B) Assertion (A) is true, Reason (R) is true but R is not the correct explanation of A.
C) A is true, R is false.
D) A is false, R is true.

Answer:
D) A is false, R is true.

Question 25.
Assertion (A) : Degree of a quadratic equation is 2.
Reason (R) : Sum of the roots of x² - px + q = 0 is p.

A) Assertion (A) is true, Reason (R) is true and R is the correct explanation of A.
B) Assertion (A) is true, Reason (R) is true but R is not the correct explanation of A.
C) A is true, R is false.
D) A is false, R is true.

Answer:
B) Assertion (A) is true, Reason (R) is true but R is not the correct explanation of A.

Question 26.
Assertion (A) : The graph representing distinct roots of a quadratic equation is

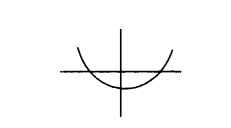
Reason (R) : Every quadratic equation has two different roots.

A) Assertion (A) is true, Reason (R) is true and R is the correct explanation of A.
B) Assertion (A) is true, Reason (R) is true but R is not the correct explanation of A.
C) A is true, R is false.
D) A is false, R is true.

Answer:
C) A is true, R is false.

Question 27.
Find the discriminant of quadratic equation x² - 5x + 6 = 0.

Solution:
Discriminant = b² - 4ac
= (-5)² - 4(1)(6)
= 25 - 24
= 1

Question 28.
Express 2y = 5x + 7 in the form of ax + by + c = 0.

Answer:
5x - 2y + 7 = 0

Question 29.
Find the zeroes of quadratic polynomial p(x) = x² - 5x + 6.

Solution:
The zeroes of quadratic polynomial p(x) = x² - 5x + 6 = 3 and 2

Question 30.
The discriminant of the quadratic equation x² - 3x + 1 = 0 is _________

Solution:
The discriminant of the quadratic equation x² - 3x + 1 = 0 is 5.

10th Class Maths Quadratic Equations 2 Marks Important Questions

Question 1.
Which of the following are quadratic equations ?

i) x² - 5x + 4 = 0
ii) x - 5/x = x²

Solution:
i) Let p(x) = x² - 5x + 4 = 0
p(x) is a quadratic polynomial because, degree of variable is a positive integer.

ii) Let f(x) = x - 5/x = x²
f(x) is not a quadratic polynomial because degree of the variable is not a positive integer.
That is 5/x = 5.x^-1
(-1 is negative integer)

Question 2.
Solve the x² - 8x + 16 = 0 by factorization method.

Solution:
Given x² - 8x + 16 = 0
x² - 4x - 4x + 16 = 0
x(x - 4) - 4(x - 4) = 0
(x - 4) (x - 4) = 0
(x - 4)² = 0
x = 4, x = 4
Therefore the roots of x² - 8x + 16 = 0 are 4 and 4.

Question 3.
Find the value of k if x = - 1/2 is a solution of 3x² + 2kx - 3 = 0.

Solution:
Given p(x) = 3x² + 2kx - 3 = 0 its solution is x = - 1/2
Put x = - 1/2 in p(x) then

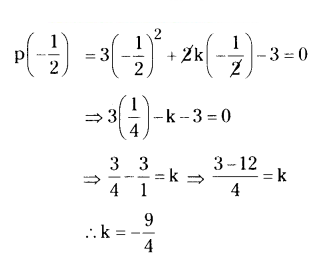
Question 4.
Find the sum and product of the roots of the quadratic equation 2x² - 9x + 4 = 0.

Solution:
Given Quadratic equation is
2x² - 9x + 4 = 0
a = 2, b = -9, c = 4
α + β = -b/a = -(-9)/2 = 9/2
αβ = c/a = 4/2 = 2

Question 5.
Find the discriminant of the quadratic equation 4x² - 5 = 0 and hence comment on the nature of roots of the equation.

Solution:
Given Quadratic equation
4x² -5 = 0
a = 4, b = 0, c = -5
b² - 4ac = 0² - 4(4) (-5) = 20 > 0
∴ Roots are real and distinct.

Question 6.
Find the roots of the quadratic equation 3x² - 7x - 6 = 0.

Solution:
Given equation 3x² - 7x - 6 = 0
a = 3, b = -7, c = -6

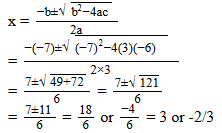
Question 7.
Find the values of k for which the equation 3x² + kx + 3 = 0 has real and equal roots.

Solution:
3x² + kx + 3 = 0
a = 3, b = k, c = 3
real and equal roots
b² - 4ac = 0
k² - 4(3) (3) = 0
k² = 4 × 3 × 3 ⇒ k = 2 × 3 ⇒ k = 6

Question 8.
Solve x² - 2ax + (a² - b²) = 0.

Solution:
Given equation x² - 2ax + (a² - b²) = 0
x² - 2ax + (a + b) (a - b) = 0
x² - (a + b) x - (a - b) x + (a + b) (a - b) = 0
x[x - (a + b)] - (a - b) (x - (a + b) = 0
(x - (a + b)) (x - (a - b)) = 0
x - (a + b) = 0 (or) x - (a - b) = 0
x = a + b or x = a - b.

Question 9.
If 2 is a root of the equation x² + kx + 12 = 0 and the equation x² + kx + q = 0 has equal roots, find the value of q.

Solution:
x² + kx + 12 = 0
2 is a root.
2² + k(2) + 12 = 0
2k + 16 = 0 ⇒ 2k = -16
k = -8
x² + kx + q = 0
2² + (-8) (2) + q = 0
4 - 16 + q = 0
q - 12 = 0
q = 12

Question 10.
Find the roots of the quadratic equation 3x² - 4√3x + 4 = 0.

Solution:
Given equation 3x² - 4√3x + 4 = 0
a = 3, b = -4√3 , c = 3

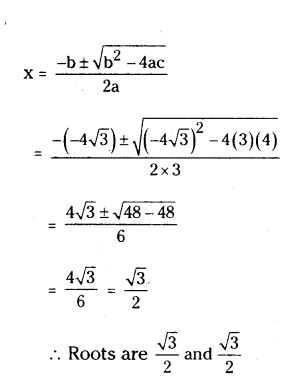
Question 11.
Solve the quadratic equation x² + 2√2x - 6 = 0.

Solution:
Given equation x² + 2√2x - 6 = 0
a = 1, b = 2√2 , c = -6

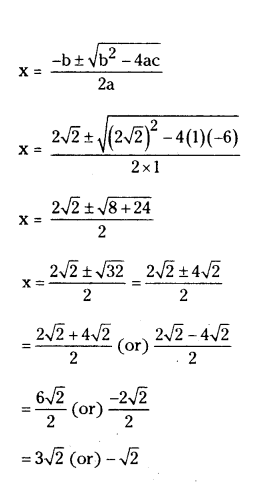
Question 12.
Find the nature of the roots of the quadratic equation :

4x² - 5x - 1 = 0.

Solution:
Given equation 4x² - 5x - 1 = 0
a = 4, b = -5, c = -1.
b² - 4ac = (-5)² - 4(4) (-1)
= 25 + 16
= 41 > 0
∴ Roots are real and distinct.

Question 13.
If b² - 4ac > 0 in ax² + bx + c = 0; then what can you say about roots of the equation ? (a ≠ 0)

Solution:
The discriminant b² - 4ac > 0 of the quadratic equation ax² + bx + c = 0 is positive. Hence its roots are real and unequal.

Question 14.
Find the value of k, if 2 is one of the roots of the quadratic equation

x² - kx + 6 = 0.

Solution:
x² - kx + 6 = 0
(2)² - k(2) + 6 = 0 .
⇒ 4 + 6 - 2k = 0
⇒ 2k = 10
⇒ k = 5

Question 15.
In a rectangle ABCD, AB = x + y, BC = x - y, CD = 9 and AD = 3. Find the values of x and y.

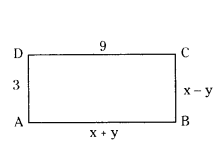
Solution:
x + y = 9; x - y = 3 (∵ two pairs of opposite sides are equal, in a rectangle)
Solving the above equations, we get x = 6 and y = 3.

Question 16.
Write the nature of roots of the qua-dratic equation 2x² - 5x + 6 = 0.

Solution:
Discriminent (D) = b² - 4ac
= (-5)² - 4(2) (6)
= 25 - 48
= -23
D < 0, So roots are not Real.

Question 17.
Write the nature of the roots of the qua-dratic equation x² - 8x + 16 = 0.

Solution:
x² - 8x + 16 = 0
Discriminent (D) = b² - 4ac
= (8)² - 4(1) (16)
= 64 - 64
= 0
Since D = 0, roots are real and equal.

Question 18.
Find sum and product of roots of the Quadratic equation

x² - 4√3x + 9 = 0

Solution:
Quadratic equation
x² - 4√3x + 9 = 0
a = 1 ; b = - 4√3 ; c = 9
Sum of roots = - b/a
= -(-4√3)/1
= 4√3
Product of roots = c/a = 9/1 = 9.

Question 19.
Find the roots of the Quadratic equation x² + 2x - 3 = 0.

Solution:
x² + 2x - 3 = 0
x² + 3x - x - 3 = 0
x(x + 3) - 1 (x + 3) = 0
(x + 3) (x - 1) = 0
x = - 3 (or) x = 1
Roots of Quadratic Equation are - 3, 1.

Question 20.
Find the values of k for which the qua-dratic equation 4x² + 5kx + 25 = 0 has equal roots.

Solution:
a = 4, b = 5k, c = 25
Q. E. has equal roots
⇒ b² - 4ac = 0
⇒ (5k)² - 4(4) (25) = 0 , 400
⇒ k² = 400/25 = 16
⇒ k = ±4.

Question 21.
Find the discriminant of the quadratic equation 3x² - 5x + 2 = 0 and hence write the nature of its roots.

Solution:
Given quadratic equation
3x² - 5x + 2 = 0
Given quadratic equation compare with ax² + bx + c = 0
Here a = 3; b = -5; c = 2
Therefore, the discriminant
b² - 4ac = (-5)² - 4(3) (2)
= 25 - 24 = 1 > 0
∴ The quadratic equation has distinct and real roots.’

Question 22.
Is (x + 2)² = x² + 3 a Quadratic equation ? Justify.

Solution:
(x + 2)² = x² + 3
x² + 4x + 4 = x² + 3
4x + 4 = 3
4x + 1 = 0
It is not a quadratic equation.

Question 23.
Construct a quadratic equation having the roots log₂8 and log₁₀100.

Solution:
log₂8 = log₂2³ = 3 log₂2 = 3 × 1 = 3
log₁₀100 = log₀10² = 2 log₁₀10 = 2 × 1= 2
So, the roots are 3 and 2.
x² - x(sum of the roots) + (product of the roots) = 0
x² - x(3 + 2) + (3 × 2) = 0
x² - 5x + 6 = 0
∴ The required quadratic equation
= x² - 5x + 6 = 0

10th Class Maths Quadratic Equations 4 Marks Important Questions

Question 1.
Solve the following quadratic equation by factorization.

i) x+3/x-2 - 1-x/x

Solution:
Given x+3/x-2 - 1-x/x = 17/4
⇒ (x+3)x-(1-x)(x-2)/(x-2)x = 17/4
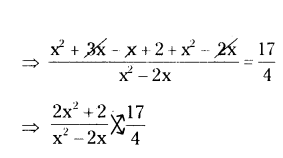By cross-multiplication
⇒ 4(2x² + 2) = 17 (x² - 2x)
⇒ 8x² + 8 = 17x² - 34x
⇒ 17x² - 8x² - 34x - 8 = 0
⇒ 9x² - 34x - 8 = 0
⇒ 9x² - 36x + 2x - 8 = 0
⇒ 9x (x - 4) + 2 (x - 4) = 0
⇒ (9x + 2) (x - 4) = 0
Therefore, x = - 2/9 (or) x = 4
So, roots of the given equation are real and not equal. They are - 2/9 and 4.

ii) 4x² - 4ax + a² - b² = 0

Solution:
Given 4x² - 4ax + a² - b² = 0
4x² - 2(a + b)x - 2(a - b)x + (a + b)(a - b) = 0
2x [x - (a + b)] - 2 (a - b) [x - (a + b)] = 0
[2x - 2 (a - b)] [x - (a + b)] = 0
2x - 2 (a - b) = 0
2x = 2(a - b)
x = 2(a-b)/2
x - (a + b) = 0
x = a + b
Therefore, x = (a - b) (or) (a + b)
So, roots of the given equation are real and not equal. They are (a - b) and (a + b).

iii) 9x² - 9 (a + b) x + (2a² + 5ab + 2b²) = 0

Solution:
Given
9x² - 9 (a + b) x + (2a² + 5ab + 2b²) = 0
9x² - [3 (2a + b) + 3 (a + 2b)] x + (2a² + 5ab + 2b²) = 0
9x² - 3 (2a + b) x - 3 (a + 2b) x + (2a + b) (a + 2b) = 0
3x [3x - (2a + b)] - (a + 2b) [3x - (2a + b)] = 0
[3x - (a + 2b)] [3x - (2a + b)] = 0
3x - (a + 2b)] = 0
3x = a + 2b
x = a+2b/3

[3x- (2a + b)] = 0
3x = 2a + b
x = 2a+b/3
Therefore, x = a+2b/3 (or) x = 2a+b/3.
So, roots of given equation are real and not equal. They are a+2b/3 and 2a+b/3.

iv) 4/k - 3 = 5/2x+3, x ≠ 0, -3/2

Solution:
Given 4/k - 3 = 5/2x+3, x ≠ 0, -3/2
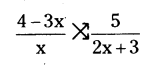By cross-multiplication
(4 - 3x) (2x + 3) = 5x
⇒ 8x + 12 - 6x² - 9x = 5x
⇒ 6x² + 5x + x - 12 = 0
⇒ 6x² + 6x - 12 = 0
⇒ 6 (x² + x - 2) = 0
⇒ x² + x - 2 = 0
⇒ x² + 2x - x - 2 = 0
⇒ x (x + 2) - 1 (x + 2) = 0
⇒ (x - 1)(x + 2) = 0
Therefore, x = 1 (or) - 2
So, roots of given equation are real and not equal. They are 1 and - 2.

Question 2.
In the following, determine whether the given quadratic equation have real roots and if so, find the roots.

√2x² + 7x + 5√2 = 0

Solution:
Given quadratic equation √2x² + 7x +5√2 = 0 is in the form of ax² + bx + c = 0
a = √2 , b = 7, c = 5√2
Discriminant = b² - 4ac
= (7)² 4√2 . 5√2
D = 49 - 40 = 9
D > 0
So, the given equation has real and distinct roots.

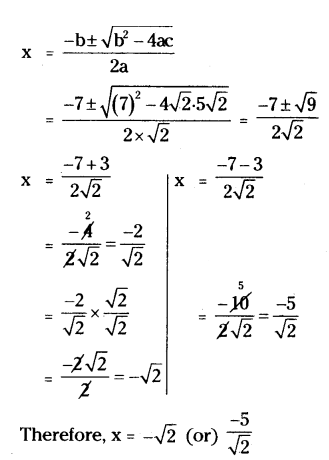
Question 3.
Find the value of k for which the given equation has real and equal roots.

i) x² - 2x (1 + 3k) + 7 (3 + 2k) = 0

Solution:
Given x² - 2x (1 + 3k) + 7 (3 + 2k) = 0 is in the form of ax² + bx + c = 0 and roots are real and equal.
a = 1, b = -2 (1 + 3k), c = 7 (3 + 2k)
Discriminant D = b² - 4ac = 0
⇒ [-2 (1 + 3k)]² - 4(1)(7)(3 + 2k) = 0
⇒ 4 (1 + 9k² + 6k) - 84 - 56k = 0
⇒ 4 + 36k² + 24k - 84 - 56k = 0
⇒ 36k² - 32k - 80 = 0
⇒ 9k² - 8k - 20 = 0
⇒ 9k² - 18k + 10k - 20 = 0
⇒ 9k (k - 2) + 10 (k - 2) = 0
⇒ (9k + 10) (k - 2) = 0
Therefore, k = -10/2 and 2.

ii) x² - 4kx + k = 0

Solution:
Given, x² - 4kx + k = 0 is in the form of ax² + bx + c = 0 and roots are real and equal.
a = 1, b = -4k, c = k
Discriminant
D = b² - 4ac = 0
⇒ (-4k)² - 4.1.k = 0
⇒ 16k² - 4k = 0
⇒ 4k (4k - 1) = 0
⇒ k = 0, 4k - 1 = 0
Therefore, k = 0 (or) 1/4

iii) kx(x - 2√5) + 10 = 0

Solution:
Given, kx(x - 2√5) + 10 = 0
kx² -x.k2√5 + 10 = 0 is in the form of ax² + bx + c = 0 and roots are real and equal.
a = k, b= -2k√5, c = 10
Discriminant (D) = b² - 4ac = 0
⇒ (-2k√5)² - 4.k.10 = 0
⇒ 4k².5 - 40k = 0
⇒ 20k² - 40k = 0
⇒ 20k (k - 2) = 0
Therefore, k = 0 (or) k = 2.

Question 4.
Solve the x² - 4ax + (4a² - b²) = 0 by factorization method.

Solution:
Given quadratic equation is
x² - 4ax + (4a² - b²) = 0
x² - [(2a - b) + (2a + b)]x + (4a² - b²) = 0
x² - (2a - b)x - (2a + b)x + (2a + b) (2a - b) = 0
x [x - (2a - b)] - (2a + b) [x - (2a - b)] = 0
[x - (2a + b)] [x - (2a - b)] = 0
(x - 2a - b) (x - 2a + b) = 0
x - 2a - b = 0 (or) x - 2a + b = 0
then x = 2a + b (or) x = 2a - b.

Question 5.
Solve a² b² x² + b²x - a²x - 1 = 0.

Solution:
Given quadratic equation is
a² b² x² + b²x - (a² x + 1) = 0.
b²x(a²x + 1) - (a²x + 1) = 0
(a² x + 1) (b² x - 1) = 0
a² x + 1 = 0 (or) b² x - 1 = 0
a²x = -1 (or) b² x = 1
x = -1/a² (or) x = 1/b²
Therefore x = - 1/a² (or) 1/b².

Question 6.
If x = 2 and 3 are roots of the equation 3x² - 2kx + 2m = 0 then find the values of k and m.

Solution:
Given x = 2 and x = 3 are solutions of
p(x) = 3x² - 2kx + 2m = 0
Put x = 2 in p(x) then
p(2) = 3(2)² - 2k(2) + 2m = 0
⇒ 3(4) - 4k + 2m = 0
⇒ -4k + 2m = -12 → (1)
Put x = 3 in p(x) then
p(3) = 3(3)² - 2k(3) + 2m = 0
⇒ 27 - 6k + 2m = 0
⇒ -6k + 2m = -27 → (2)
Subtract (1) from (2)
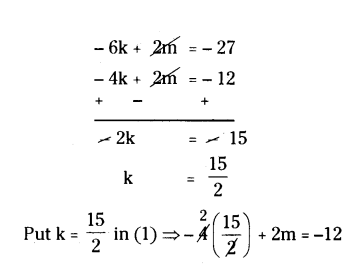⇒ -30 + 2m = -12
⇒ 2m = -12 + 30 = 18
∴ m = 18/2 = 9
∴ m = 9 and k = 15/2

Question 7.
Determine whether the given values are solution of given equation or not.

i) 6x² - x - 2 = 0, x = -1/2, x = 2/3
ii) x² - x + 1 = 0, x = 0, x = -1

Solution:
i) Given p(x) = 6x² - x - 2 = 0
Put x = -1/2 in p(x)
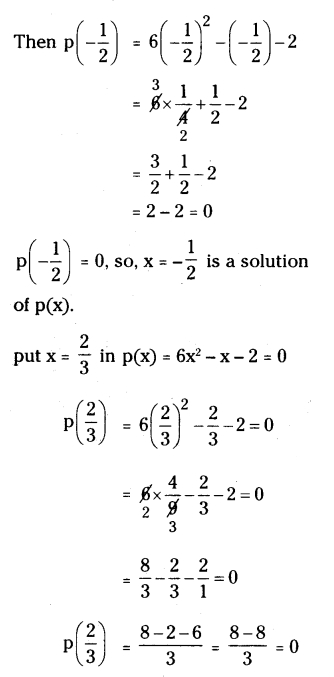LHS = RHS
So, x = 2/3 is a solution of p(x).

ii) Given f(x) = x² - x + 1 = 0
Put x = 0 in f(x) then
f(1) = 1² - 1 + 1
= 1 - 1 + 1 = 1 ≠ 0
f(1) = 1
∴ LHS ≠ RHS.
So, x = 0 is not a solution of f(x).
Put x = -1 in f(x) then
f(-1) = (-1)² - (-1) + 1= 0
= 1 + 1 + 1 =0
f(-1) = 3 ≠ 0
LHS ≠ RHS
So, x = -1 is not a solution of f(x).

Question 8.
Find the value of ‘p’ for which the quadratic equation px(x - 2) + 6 = 0 has two equal real roots.

Solution:
Given equation px(x - 2) + 6 = 0
px² - 2px + 6 = 0
a = p, b = -2p, c = 6.
b² - 4ac = (-2p)² - 4(p) (6) = 0
4p² - 24p = 0
4p² = 24p
p = 6

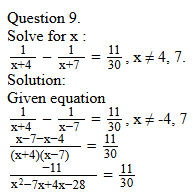
-30 = x² - 3x - 28
x² - 3x - 28 + 30 = 0
x² - 3x + 2 = 0
x² - 2x - x + 2 = 0
x(x - 2) + 1(x - 2) = 0
(x - 2) (x + 1) = 0
x = 2 or -1.

Question 10.
In a flight of 600 km, an aircraft was slowed due to bad weather. Its average speed for the trip was reduce by 200 km/h and time of flight increased by 30 minutes. Find the original duration of flight.

Solution:
Let the original speed of the aircraft = x kmph.
Let the new speed = (x - 200) km/hr
Duration of flight at original speed = (600/x) hr.
Duration of flight at reduced speed = (600/x-200) hr.
∴ 600/x-200 = 600/k = 1/2
600x-600(x-20)/x(x-200) = 1/2
120000/x2-200x = 1/2
⇒ x² - 200x - 240000 = 0
⇒ x² - 600x + 400x - 240000 = 0
(x - 600) (x + 400) = 0
x = 600 (or) x = -400
x = 600
The original speed of the aircraft was 600 km/hr
duration of flight = 600/x hr = (600/60) hr = 1 hr

Question 11.
The sum of the squares of three positive numbers that are consecutive multiples of 5 is 725. Find the three numbers.

Solution:
Let the first number be 5x
second number 5x + 5 = 5(x + 1)
third number 5x + 10 = 5(x + 2)
∴ (5x)² + [5(x + 1)]² + [5(x + 2)]² = 725
25x² + 25(x² + 2x + 1) + 25(x² + 4x + 4) = 725
25 [x² + x² + 2x + 1 + x² + 4x + 4] = 725
3x² + 6x + 5 = 725/25
3x² + 6x + 5 = 29
3x² + 6x - 24 = 0
3(x² + 2x - 8) = 0
x² + 2x - 8 = 0
x² + 4x - 2x - 8 = 0
x(x + 4) - 2 (x + 4) = 0
(x + 4) (x - 2) = 0
x + 4 = 0 (or) x - 2 = 0
x = -4 or x = 2
∴ First number = 5x = 5 × 2 = 10
Second number = 10 + 5 = 15
Third number = 10 + 10 = 20

Question 12.
A motor boat whose speed in still water is 18 km/h, takes 1 hour more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream.

Solution:
Speed of boat =18 kmph
Distance = 84 km

For upstream:
Speed = (18 - x) kmph
Distance = 24 km
Time = t₁
t₁ = 24/18-x

For downstream:
Speed = (18 + x) kmph
Distance = 24 km
Time = t₂
t₂ = 24/18+x
∴ t₁ = t₂ + 1
24/18-x = 24/18+x + 1/1
1/18-x = 1/18+x = 12/4
(18+x)-(18-x)/(18-x)(18+x) = 12/4
48x = (18 - x) (18 + x)
48x = 324 + 18x - 18x - x²
x² + 48x - 324 = 0
x² + 54x - 6x - 324 = 0
x(x + 54) - 6(x + 54) = 0
(x + 54) (x - 6) = 0
x = -54 or x = 6.
but x = 6 only
∴ Speed of stream = 6 kmph.

Question 13.
Places A and B are 80 km from each other on a highway. A car starts from A and another from B of the same time. If they more in same direction they meet in 8 hours and if they move towards each other they meet in 1 hour 20 minutes. Find the speed of cars.

Solution:
Let speed of car starting from A be x kmph
Let speed of car starting from B be y kmph
Total distance = 80 km
1 hr 20 min = 1 + 20/60 hr = 1 + 1/3 = 4/3 hr
When car moves in same direction they will meet in 8 hours
Distance travelled from B = 8y km
Distance travelled from A = 8x km
∴ 8x - 8y = 80
x - y = 10 .... (1)
When car moves in opposite direction they will meet in 1 hr 20 min.
Distance travelled from A = 4x/3
Distance travelled from B = 4y/3
Total distance covered = 4x/3 + 4x/3
80 = 4x/3 + 4x/3
240 = 4x + 4y
∴ x + y = 60
x + y = 60
x - y = 10
2x = 70
x = 35

y = 60 - 35
y = 25
Speed of car starting from A = 35 kmph
Speed of car starting from B = 25 kmph.

Question 14.
The sum of two numbers is 15. If the sum of their reciprocals is 3/10, find the two numbers.

Solution:
Let the first number be x
Other number = 15 - x
∴ 1/x + 1/15-x = 3/10
10(15 - x + x) = 3(x(15 - x))
150 = 45x - 3x²
3x² - 45x + 150 = 0
x² - 15x + 50 = 0
x² - 10x - 5x + 50 = 0
(x - 10) (x - 5) = 0
x = 10 or 5.
∴ Required number are 5 and 10.

Question 15.
Rohan’s mother Is 26 years older than him. The product of their ages after 3 years will be 360 years. Write the quadratic equation to find Rohan’s present age.

Solution:
Let Rohan’s present age = x years
Rohan’s mothers present age = x + 26 years
After 3 years Rohan’s age = x + 3 years
After 3 years Rohan’s mothers age = x + 29 years
By the problem
(x + 3) (x + 29) = 360
⇒ x² + 32x + 87 = 360
⇒ x² + 32x - 273 = 0

Question 16.
If 9x² + kx + 1 = 0 has equal roots, find the value of k.

Solution:
We know the roots of a quadratic equation are equal if and only if its discriminant is zero.
i.e. for ax² + bx + c = 0, b² - 4ac = 0 here a = 9, b = k, c = 1
then b² - 4ac = 0 becomes
k² - 4.9.1 = 0
⇒ k² - 36 = 0
∴ k² = 36 and k = √36 = ± 6
So k = ± 6.

Question 17.
If the measure of angles of a triangle are x°, y° and 40°, and difference between the two measures of angles x° and y° is 30°, then find the values of x° and y°.

Solution:
x + y + 40 = 180°
(∵ sum of angles of a triangle is 180°)
x + y = 140 _______ (1)
x - y = 30 _______ (2)
(1) and (2)
Solving the equations we obtain
x = 85°, y = 55°

Question 18.
The sum of a number and its reciprocal is 10/3. Find the number.

Solution:
Let the number be ‘x’
Its reciprocal is 1/x
x + 1/x = 10/3, the quadratic equation obtained from this is 3x² - 10x + 3 = 0
After solving, we get x = 3 or 1/3
∴ Required number is 3 or 1/3.

Question 19.
Find the roots of quadratic equation x² + 4x + 3 = 0 by "Completing Square method".

Solution:
Given quadratic equation is
x² + 4x + 3 = 0
x² + 4x = -3
x² + 2.x.2 = -3
Now LHS is of the form a² + 2ab, where b = 2.
Adding b² = 2² on both sides, we get
x² + 2(x) (2) + (2)² = -3 + (2)²
(x + 2)² = -3 + 4
(x + 2)² = 1
x + 2 = ± 1
x + 2 = 1 ; x + 2 = -1
x = 1 - 2 = -1 ; x = -1 -2 = -3
∴ -1, -3 are the roots of the given Q.E.

Question 20.
Write a Quadratic equation, whose roots are 3 + √5 and 3 - √5.

Solution:
Roots are 3 + √5, 3 - √5.
Sum of the roots = (3 + √5) + (3 - √5)
= 6
Product of roots = (3 + √5) (3 - √5)
= 9 - 5 = 4
∴ Required Quadratic equation
= x² - x (sum of the roots) + Product of roots = 0
x² - 6x + 4 = 0

Question 21.
A strip of width 4 cm is attached to one side of a sqaure to form a rectangle. The area of the rectangle formed is 77 cm², then find the length of the side of the square.

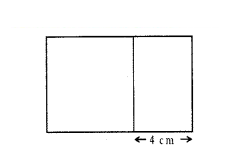
Solution:
Let the side of the square be ‘x’ cm.
Then length of rectangle = x + 4 cm
Breadth of rectangle = x cm
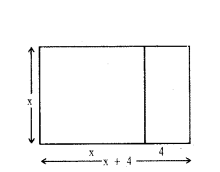Area of rectangle = length × breadth
= (x + 4)x
But as per given problem, area of rectangle = 77 cm²
∴ x(x + 4) = 77
x² + 4x - 77 = 0
x² + 11x - 7x - 77 = 0
x(x + 11) - 7(x + 11) = 0
(x + 11) (x - 7) = 0
x + 11 = 0 (or) x - 7 = 0
x = - 11 (or) x = 7
but ‘x’ can’t be negative, so x = 7
∴ Length of the side of the square = 7 cm

Question 22.
If one root of the quadratic equation 3x² - 8x - (2k + 1) = 0 is seven times the other, then find the value of k.

Solution:
Given equation
3x² - 8x - (2k + 1) = 0
Let the roots are α and 7α.
a = 3, b = -8, c = - 2k - 1
α + 7α = -b/a = - -(-8)/3
8α = 8/3
α 1/3
α × 7α = c/a
7α² = -2k-1/3
7(1/3)² -2k-1/3
7/9 = -2k-1/3 7/3 = - 2k - 1
7 = - 6k -3
7 + 3 = -6k
10 = -6k
k = 10/-6 = 5/-3

10th Class Maths Quadratic Equations 8 Marks Important Questions

Question 1.
A two digit number in such that the product of its digits is 18, when 63 is subtracted from the number, the digits interchange their places. Find the number.

Solution:
Let the digit in the tens place be x .
Then units digit = 18/x
Now number = 10.x + 18/x
If we interchange the digits, then the number 10.18/x + x
Given that
⇒ (10x + 18/x) - (10.18/x + x) = 63 ⇒ 10x2+18/x - (180+x2/x) = 63 ⇒ 10x2+18-180-x2/x = 63
⇒ 9x² - 162 = 63x
⇒ 9x² - 63x - 162 = 0
⇒ 9 (x² - 7x - 18) = 0
⇒ x² - 7x - 18 = 0
⇒ x² - 9x + 2x - 18 = 0
⇒ x (x - 9) + 2 (x - 9) = 0
⇒ (x + 2) (x - 9) = 0
⇒ x = -2 (or) 9.
Digit can never be negative.
So, digit in tens place x = +9
Digit in ones place = 18/x = 18/9= 2
∴ Number = 10 × x + 18/x
= 10 × 9 + 18/9 = 92

Question 2.
Three consecutive positive integers are such that the sum of the square of the first and the product of other two is 46. FInd the integers.

Solution:
Let the three consecutive integers are (x - 1),xand (x + 1).
Square of first + Product of other two = 46
⇒ (x - 1)² + x (x + 1) = 46
⇒ x² - 2x + 1 + x² + x = 46
⇒ 2x² - x + 1 - 46 = 0
⇒ 2x² - x - 45 = 0
⇒ 2x² - 10x + 9x - 45 = 0
⇒ 2x (x - 5) + 9 (x - 5) = 0
⇒ (2x + 9) (x - 5) = 0 -9
Therefore, x = -9/2 (or) 5
-9/2 can never be integer.
So, x = 5.
Integers are (x - 1), x, (x + 1)
(5 - 1), 5, (5 + 1)
4, 5, 6
∴ Integers are 4, 5 and 6.

Question 3.
While boarding an aeroplane, a passenger got hurt. The pilot showing promptness and concern, made arrangements to hospitalise the injured and so the plane started late by 30 minutes to reach the destination, 1500 km away in time, the pilot increased the speed by 100 km/h. Find the original speed per hour of the plane.

Solution:
Let the speed of plane in the beginning x kmph.
Time = Distance/Speed
t₁ = 1500/x hours
If pilot increased the speed by 100 kmph.
So, t₂ = 1500/x+100
Now, t₁ - t₂ = 30 minutes = 1/2 an hour
1500/x - 1500/x+100 = 1/2
1500 [ x+100-x/x(x+100) ] = 1/2
⇒ 150000 × 2 = x (x + 100)
⇒ 300000 = x² + 100x
⇒ x² + 100x - 300000 = 0
⇒ x² + 600x - 500x - 300000 = 0
⇒ x (x + 600) - 500 (x + 600) = 0
⇒ (x - 500) (x + 600) = 0
⇒ x = 500 (or) -600.
Speed can never be negative.
Therefore, speed of the plane in the beginning is 500 kmph.

Question 4.
A girl is twice as old as her sister. Four years hence, the product of their ages will be 160. Find their present ages.

Solution:
Let the girl’s present age be x years.
Sister’s age = 2x years.
Four years hence, girl’s age = (x + 4) years.
and sister’s age = (2x + 4) years.
Product of their ages = 160
⇒ (x + 4) (2x + 4) = 160
⇒ 2x² + 4x + 8x + 16 = 160
⇒ 2x² + 12x + 16 -160 = 0
⇒ 2x² + 12x - 144 = 0
⇒ 2 (x² + 6x - 72) = 0
⇒ x² + 6x - 72 = 0
⇒ x² + 12x - 6x - 72 = 0
⇒ x (x + 12) - 6 (x + 12) = 0
⇒ (x - 6) (x + 12) = 0
x = 6 (or) -12
Age can never be negative.
Therefore, present age of girl x = 6 years.
Sister’s age = 2x = 2 (6) = 12 years.

Question 5.
Sum of the areas of two squares is 640 m². If the difference of their perimeters is 64 m. Find the sides of the two squares.

Solution:
Let the sides of the squares be x m and y m.
Then their areas are x² and y² m².
Given, sum of areas = 640 m²
⇒ x² + y² = 640 m²
⇒ y² = 640 - x² → (1)
Difference of their perimeters = 64 m
⇒ 4x - 4y = 64
⇒ 4 (x - y) = 64
⇒ x - y = 16
⇒ y = x - 16 → (2)
Put (2) in (1)
⇒ (x - 16)² = 640 - x²
⇒ x² + 256 - 32x = 640 - x²
⇒ x² - 32x + 256 + x² - 640 = 0
⇒ 2x² - 32x - 384 = 0
⇒ 2 (x² - 16x - 192) = 0
⇒ x² - 16x- 192 = 0
⇒ x² - 24x + 8x - 192 = 0
⇒ x (x - 24) + 8 (x - 24) = 0
⇒ (x + 8) (x - 24) = 0
⇒ x = - 8 (or) 24.
Length can never be negative.
Therefore, side of one square is x = 24 m.
Side of other square y = x - 16 y = 24 - 16 = 8 m
∴ Sides of squares are 24 m and 8 m.

Question 6.
Sum of the areas of two squares is 400 cm². If the difference of their perimeter is

16 cm, find the sides of two squares.

Solution:
Let sides of the squares are x cm and y cm.
Then their areas are x² cm² and y² cm².
Sum of areas = x² + y² = 400 cm² → (1)
Difference of their perimeters = 16 cm
⇒ 4x - 4y = 16 cm
⇒ 4 (x - y) = 16
⇒ x - y = 4
⇒ y = x - 4 → (2)
Put (2) in (1)
⇒ x² + (x - 4)² = 400
⇒ x² + x² - 8x + 16 = 400
⇒ 2x² - 8x + 16 - 400 = 0
⇒ 2x² - 8x - 384 = 0
⇒ 2 (x² - 4x - 192) = 0
⇒ x² - 4x - 192 = 0
⇒ x² - 16x + 12x - 192 = 0
⇒ x(x - 16) + 12(x - 16) = 0
⇒ (x + 12)(x - 16) = 0
Therefore, x = -12 (or) 16
Length can never be negative.
So, side of the square x = 16 cm
Side of the other square y = x - 4
= 16 - 4 = 12 cm

Question 7.
In a class test, the sum of Shefali’s marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product of her marks would have been 210. Find her marks in two subjects.

Solution:
Let the marks in Mathematics = x
Marks in English = y
Sum of the marks x + y = 30 y = 30 - x
Two marks more in Maths = x + 2
Three marks less in English = 30 - x - 3
= 27 - x
Product = (x + 2) (27 - x) = 210
⇒ 27x - x² + 54 - 2x = 210
⇒ 25x - x² + 54 - 210 = 0
⇒ x² - 25x - 54 + 210 = 0
⇒ x² - 25x + 156 = 0
⇒ x² - 13x - 12x + 156 = 0
⇒ x (x - 13) - 12 (x - 13) = 0
⇒ (x- 12) (x - 13) = 0
Therefore, x = 12 (or) 13.
Marks in Maths x = 12
Marks in English y = 30 - x
= 30 - 12 = 18

Question 8.
Solve x + 1/x = 25 1/25

Solution:
Given quadratic equation is

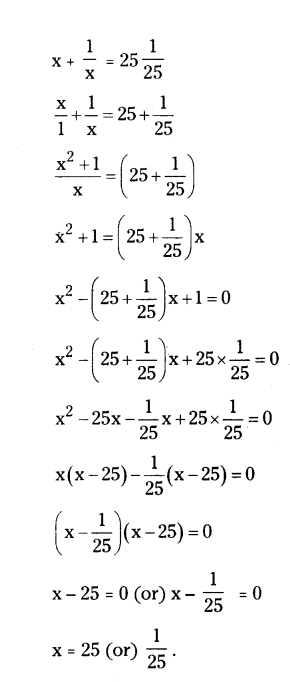
Question 9.
A train travels a distance of 300 km at constant speed. If the speed of the train is increased by 5 kin per hour, the journey would have taken 2 hours less. Find the speed of the train.

Solution:
Let the constant speed of the train be x km/hour.
Time taken to travel the 300 km distance (t₁) = 300/x hours.
If the speed of the train increased by 5 km.
Then time taken to travel the 300 km (t₂) = 300/x+5 hour.
difference t₁ - t₂ = 2 hours
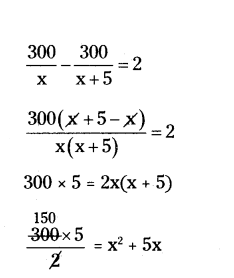750 = x² + 5x
x² + 5x - 750 = 0
x² + 30x - 25x - 750 = 0
x(x + 30) - 25(x + 30) =0
(x - 25) (x + 30) = 0
x - 25 = 0 (or) x + 30 = 0
x = 25 (or) x = -30
Speed cannot be negative.
Therefore constant speed of the train is 25 kmph.

Question 10.
The sum of the ages of father and his son is 45 years. Five years ago, the product of their ages was 124. Determine their present ages.

Solution:
Let the present age of father be x years
then the son’s age = (45 - x) years
Five years ago, father’s age = (x - 5) years
Son’s age = 45 - x - 5 = (40 - x) years
Given the product of their ages = 124
(x - 5) (40 - x) = 124
40x - x² - 200 + 5x = 124
x² - 45x + 200 + 124 = 0
x² - 45x + 324 = p
x² - 36x - 9x + 324 = 0
x(x - 36) - 9(x - 36) = 0
(x - 9) (x - 36) = 0
x - 9 = 0 (or) x - 36 = 0
x = 9 (or) x = 36
Therefore x = 9 (or) 36
If father’s age 9 years is not possible.
So, fathers present age = 36 years
Son’s present age = 45 - 36 = 9 years.

Question 11.
The hypotenuse of a grassy land in the shape of a right triangle is 1 metre more than twice the shortest side. If the third side is 7 m more than die shortest side. Find the sides of the grassy land.

Solution:
Let the shortest side be x m.
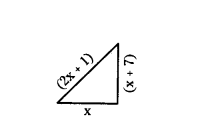then hypotenuse = twice the shortest side + 1 = (2x + 1) m
Third side = shortest side + 7 = x + 7
by Pythagoras theorem, (hypotenuse)²
= (Shortest side)² + (Third side)²
(2x + 1)² = x² + (x + 7)²
4x² + 4x + 1 = x² + x² + 14x + 49
4x² - 2x² + 4x - 14x + 1 - 49 = 0
2x² - 10x - 48 = 0
2(x² - 5x - 24) = 0
x² - 5x - 24 = 0
x² - 8x + 3x - 24 = 0
x(x - 8) + 3(x - 8) = 0
(x + 3) (x - 8) = 0
x + 3 = 0 (or) x - 8 = 0
x = - 3 (or) x = 8
Side of land cannot be negative.
So, shortest side x = 8 m
Hypotenuse = 2(8) + 1 = 16 + 1 = 17m
Third side = 8 + 7 = 15 m
Therefore, sides of the grassy land are 8 m, 15 m and 17 m.

Question 12.
Sum of the squares of two consecutive positive even integers is 100; find those numbers by using quadratic equations.

Solution:
Let the first positive even number = x say
Then its square = x²
The consecutive even number = x + 2
Then square of it = (x + 2)²
Sum of squares of above two
= (x)² + (x + 2)² = 100
∴ x² + x² + 4x + 4 = 100
2x² + 4x + 4 - 100 = 0
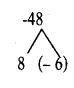⇒ 2x + 4x - 96 = 0
∴ x² + 2x - 48 = 0
⇒ x² + 8x - 6x - 48 = 0
x(x + 8) - 6(x + 8) = 0
∴ (x - 6) (x + 8) = 0
⇒ x - 6 = 0 or x + 8 = 0
⇒ x = 6 or x = -8
We consider x = 6 only because it is a positive even
⇒ x + 2 = 6 + 2 = 8
Then the given numbers are 6 and 8
Verification:
6² + 8² = 36 + 64 = 100. So verified.

Question 13.
Sum of the areas of two squares is 850 m². If the difference of their perimeters is 40 m, find the sides of the two squares.

Solution:
Let the side of first square be ‘a’
the side of second square be ‘b’
Area of first square = ‘a²‘ m²
Area of second square = ’b²‘ m²
Sum of the area of two squares = 850 m²
a² + b² = 850 ..... (1)
Perimeter of first square = ‘4a’m
Perimeter of second square = ‘4b’ m
Difference of their perimeters = 40 m
4a - 4b = 40
a - b = 10 ....... (2)
a = b + 10
substitute this in eqn (1)
(b + 10)² + b² = 850
b² + 20b + 100 + b² = 850
2b² + 20b - 750 = 0
b² + 10b - 375 = 0
b² + 25b - 15b - 375 = 0
b(b + 25) - 15(b + 25) = 0
(b - 15)(b + 25) = 0
b = 15, b = -25
from (2) a - 15 = 10
⇒ a = 25
∴ The sides of two squares are 25m, 15m.

Question 14.
A train travels 360 km at a uniform speed. If the speed had been 5 km/h more, it would have taken 1 hour less for the same journey. Find the speed of the train.

Solution:
The distance travelled = 360 km
Let the speed of the train = x kmph
Time taken to complete a journey = distance/speed
By problem 360/x - 360/x+5 = 1 = 1
360(1/x - 1/x+5) = 1
360(x+5-x/x(x+5)) = 1 = 1
⇒ 5/x2+5x - 1/360) = 1
x² + 5x - 1800 = 0
x² + 45x - 40x - 1800 = 0
x (x + 45) - 40 (x + 45) = 0
(x + 45) (x - 40) = 0
x + 45 = 0 (or) x - 40 = 0
x = -45 or x = + 40
But x can’t be negative.
∴ The speed of the train = 40 kmph

AP 10th Class Maths 5th Lesson Important Questions and Answers Quadratic Equations

Question 1.
If b² - 4ac ≥ 0, then write the roots of a quadratic equation ax² + bx + c = 0

Solution:
When b² - 4ac ≥ 0 then the roots of given quadratic equation ax² + bx + c = 0 are

Question 3.
Two angles are complementary and one angle is 18° more than tne other, then find angles.

Solution:
Let smaller angle be x°
bigger angle be y°
Since these two angles are comple-mentary
x + y = 90° .... (1)
Since bigger angle is more than smaller angle
by 18°, y - x = 18° .....(2)
By solving (1) & (2), we get x = 36°, y = 54°

Question 4.
Find the discriminant of the quadratic equation 2x² - 4x + 3 = 0.

Solution:
Discriminant of standard quadratic equation
ax² + bx + c = 0 is b² - 4ac
Now comparing the given quadratic equation 2x² - 4x + 3 = 0 with stan¬dard form of quadratic equation.
We get a = 2, b = -4, c = 3 then its discriminant = b² - 4ac
= (-4)² - 4(2) (3)
= 16 - 24 = -8
∴ Discriminant = -8.

Question 1.
Find the roots of x + 6/x = 7, x ≠ 0

Solution:
x + 6/x = 7 ⇒ x2+6/x = 7
⇒ x² - 7x + 6 =0
⇒ (x - 6) (x - 1) = 0
⇒ x = 6 or 1
Roots = 6, 1

Question 2.
Length of a rectangle is 2 units greater than its breadth. If the area of the rect-angle is 120 sq. units then find its length.

Solution:
Let breadth of the rectangle = x
Length = x + 2 ,
Area = 120 sq. units
x(x+2) = 120
x2 + 2x- 120 = 0
(x + 12) (x- 10) = 0
x = - 12 or 10
Breadth cannot be negative
∴ Breadth of the rectangle = x
= 10 units
∴ Length = x + 2 = 10 + 2 = 12 units

Question 3.
Find the zeroes of the quadratic poly-nomial x² - x - 30 and verify the rela¬tion between the zeroes and its co¬efficients.

Solution:
Given quadratic polynomial = x² - x - 30
⇒ x² - x - 30 = 0 = 0
x² - 6x + 5x - 30 = 0
⇒ x(x - 6) + 5(x - 6) = 0
⇒ (x - 6) (x + 5) = 0
⇒ x - 6 = 0
x = 6
x + 5 = 0 x = -5
∴ Zeroes are α = 6 and β = - 5
Sum of zeroes = α + β = -b/a
⇒ 6 - 5 = -(-1)/1
⇒ 1 = 1
Product of zeroes α + β = 6(-5) = c/a
= -30 = -30/1
Hence the relation was verified.

Question 4.
Find the roots of the quadratic equa¬tion (3x - 2)² - 4(3x - 2) + 3 = 0.

Solution:
(3x - 2)² - 4(3x - 2) + 3 = 0
9x² + 4 - 12x - 12x + 8 + 3 = 0
9x² - 24x +15 = 0
3x² - 8x + 5 = 0
3x² - 3x - 5x + 5 = 0
3x(x - 1) - 5 (x - 1) = 0
(x- 1) (3x - 5) = 0
x = 1 (or) x = 5/3
Roots of quadratic equation are 1, 5/3.

Question 5.
Two numbers differ by 4 and their product is 192. Find the numbers.

Solution:
Let the larger number be ‘x’
Since the difference of two numbers is 4,
Then the smaller number is (x - 4)
Their product = x(x - 4)
Given that product = 192
∴ x(x - 4) = 192
⇒ x² - 4x - 192 = 0
⇒ x² - 16x + 12x- 192 = 0
⇒ x(x - 16) + 12(x - 16) = 0
⇒ (x - 16)(x + 12) = 0
⇒ x = 16 or x = -12
If x = 16, then x - 4 = 16 - 4 = 12
then the numbers are 16 and 12.
If x = - 12, thenx-4 = - 12 - 4 = - 16
then the numbers are - 12 and - 16.

Question 1.
Find the roots of the equation 5x² - 7x - 6 = 0 by the method of completing the square.

Solution:
Given that 5x² - 7x - 6 = 0
5x² - 7x = 6
x² - 75/x = 6/5
⇒ x².2. 7/10 x = 6/5
adding 49/100 on the both sides
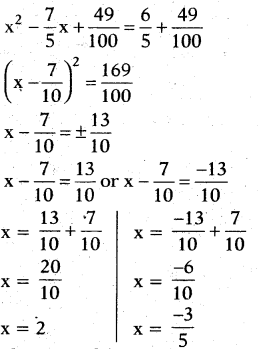The roots of the quadratic equation are 2 and -3/5

Question 2.
Find the roots of the quadratic equation 3x² + 11x + 10 = 0 by method of - completing the Square.

Solution:
Given : 3x² + 11x + 10 = 0
Dividing both sides by 3.

Question 3.
Solve the Quadratic equation 9x² - 9x + 2 = 0 by the method of com-pleting the square.

Solution:
Given : 9x² - 9x + 2 = 0
⇒ x² - x + 2/9 = 0
⇒ x² - x = - 2/9